【練習問題】
つぎの3つの式によって示される直線と放物線は、図のように平面を9つの領域に分ける。
ア y=-x2+9
イ y=x+5
ウ y=0
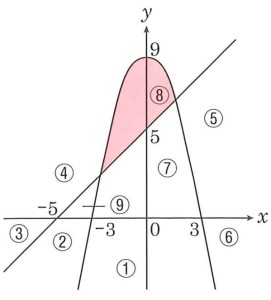 これらの領域は、上のア、イ、ウの各式の等号を適宜不等号に置き換えて得られる1組の連立不等式によって示される。ただし、領域に図中の太い境界線は含まれないものとする。
これらの領域は、上のア、イ、ウの各式の等号を適宜不等号に置き換えて得られる1組の連立不等式によって示される。ただし、領域に図中の太い境界線は含まれないものとする。
【1】ア、イ、ウの式の等号を全て不等号に置き換えて、⑧の領域(図の斜線部分)を表したとすると、左開きの不等号(>)がつくのは、ア、イ、ウのうちどれか。AからHまでの中から1つ選びなさい。
A アだけ
B イだけ
C ウだけ
D アとイの両方
E アとウの両方
F イとウの両方
G アとイとウのすべて
H ア、イ、ウのいずれにもつかない
【2】つぎの3式からなる連立不等式によって表される領域は、①から⑨のうちどれか。AからJまでの中から1つ選びなさい。
ア y>-x2+9
イ y<x+5
ウ y<0
A ②の領域
B ④の領域
C ⑤の領域
D ⑥の領域
E ②と⑥の領域
F ②と⑨の領域
G ③と④の領域
H ⑤と⑨の領域
I 3式で表される領域は存在しない
J AからIのいずれでもない